850. Rectangle Area II

850. Rectangle Area II

We are given a list of (axis-aligned) rectangles.  Each rectangle[i] = [x1, y1, x2, y2] , where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the ith rectangle.

Find the total area covered by all rectangles in the plane.  Since the answer may be too large, return it modulo 10^9 + 7.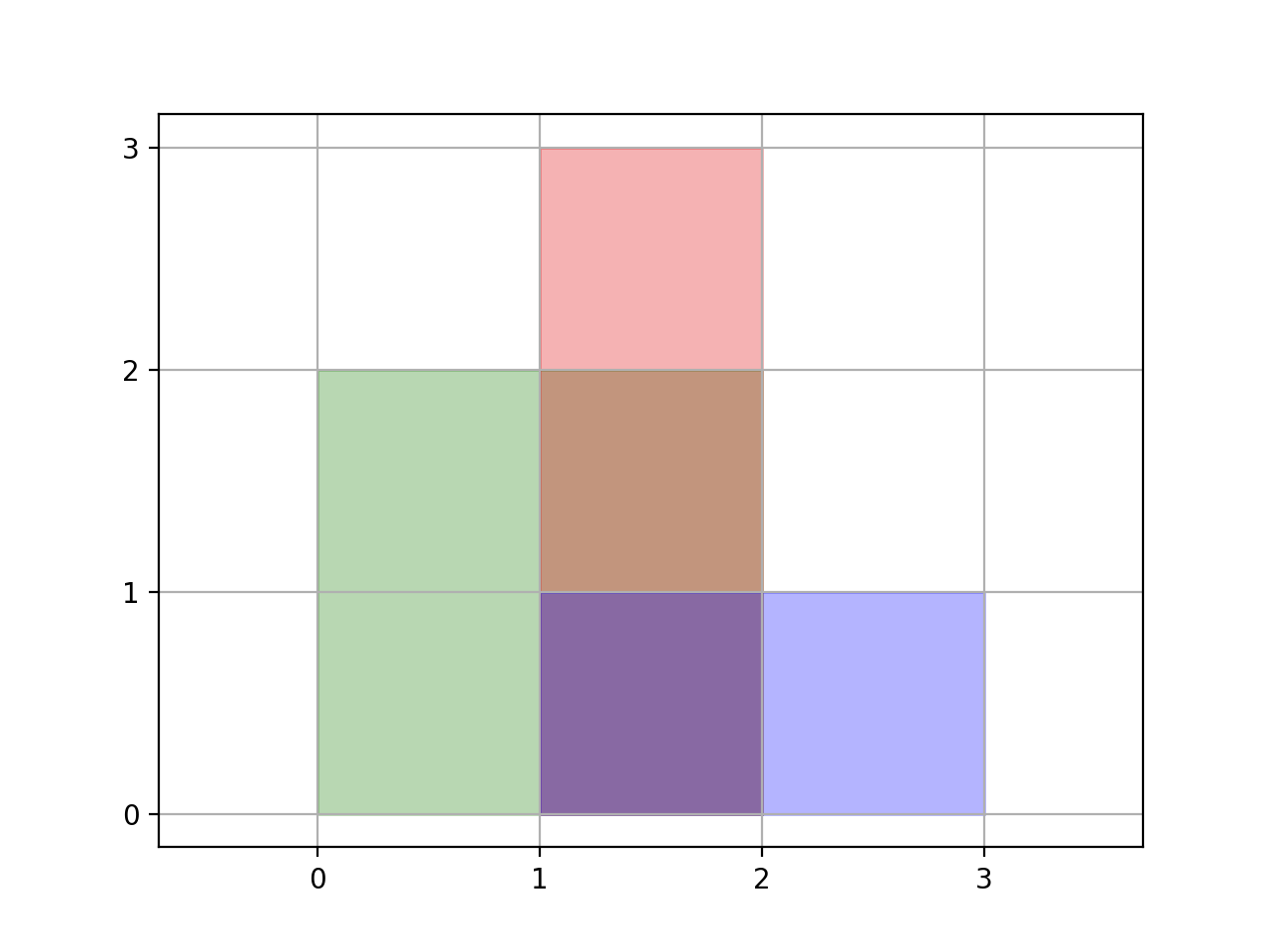

Example 1:

Input: [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
Explanation: As illustrated in the picture.

Example 2:

Input: [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 10^18 modulo (10^9 + 7), which is (10^9)^2 = (-7)^2 = 49.

Note:

• 1 <= rectangles.length <= 200
• rectanges[i].length = 4
• 0 <= rectangles[i][j] <= 10^9
• The total area covered by all rectangles will never exceed 2^63 - 1 and thus will fit in a 64-bit signed integer.

------------------------------
先按x坐标扫描，每次计算[x1，x2]上的面积大小。一共计算2 ＊ n次
计算过程是对所有在[x1, x2]内的图形进行切割，剩下的塞回去。然后再对y轴进行排列，然后求和。

O(n * n * lg n) time
想法: 如果排序的时候考虑到y轴，那可以去掉第2步的排序，并且把切割完的图形不塞回priority queue里，这样可以优化到O(n * n)

class Solution {
    public int rectangleArea(int[][] rectangles) {
        PriorityQueue<int[]> que = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        for (int[] rec : rectangles) que.add(rec);
        
        long sum = 0;
        
        while (!que.isEmpty()) {
            List<int[]> batch = new ArrayList<>();
            int[] cur = que.poll();
            batch.add(cur);
            while (!que.isEmpty() && que.peek()[0] == cur[0]) {
                batch.add(que.poll());
            }
            
            verticalCut(batch, que);
            sum += (long)getSum(batch) * (batch.get(0)[2] - batch.get(0)[0]);
        }
        
        return (int)(sum % (1000000000 + 7));
    }
    
    private int getSum(List<int[]> batch) {
        Collections.sort(batch, (a, b) -> a[1] - b[1]);
        List<int[]> temp = new ArrayList<>();
        
        temp.add(batch.get(0));
        int i = 1;
        while (i < batch.size()) {
            int[] cur = batch.get(i);
            int[] end = temp.get(temp.size() - 1);
            if (cur[1] <= end[3]) {
                end[3] = Math.max(end[3], cur[3]);
            }else {
                temp.add(cur);
            }
            
            i++;
        }
        
        int sum = 0;
        for (int[] t : temp) {
            sum += t[3] - t[1];
        }
        
        return sum;
    }
    
    private void verticalCut(List<int[]> batch, PriorityQueue<int[]> que) {
        int min = que.isEmpty() ? batch.get(0)[2] : que.peek()[0];

        for (int[] rec : batch) {
            min = Math.min(min, rec[2]);
        }
        
        for (int[] rec : batch) {
            if (rec[2] > min) {
                int[] right = new int[]{min, rec[1], rec[2], rec[3]};
                rec[2] = min;
                que.add(right);
            }
        }
    }
}

Solution #2
Ref: https://leetcode.com/problems/rectangle-area-ii/discuss/139835/TopJava-Solution-with-detailed-explaination-check-this-one-!

1. 存线段的话还是不能解决当x点时的情况，所以只能存点
2. 点的val是为了更方便的计算进出。因为左下是1，所以右下跟左上只能设为-1，从而右上只能设为1
3. preY是只计算矩形左边的边
4. getY里的count是为了计算当前进出
5. 用ide跑几个test case就能明白代码

O(n^2)

class Solution {
    class Point {
        public int x;
        public int y;
        public int val;
        public Point(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
    }
    
    public int rectangleArea(int[][] rectangles) {
        
        List<Point> points = new ArrayList<>();
        
        for (int[] r : rectangles) {
            int x1 = r[0], x2 = r[2],y1 = r[1], y2 = r[3];
            points.add(new Point(x1,y1, 1));
            points.add(new Point(x1,y2, -1));
            points.add(new Point(x2,y1, -1));
            points.add(new Point(x2,y2, 1));
        }
        
        Collections.sort(points, (a, b) -> {
            return a.x - b.x;
        });
        
        Map<Integer, Integer> map = new TreeMap<>();
        int preX = -1, preY = -1;
        int rt = 0;
        for (int i = 0; i < points.size(); i++) {
            Point p = points.get(i);
            map.put(p.y, map.getOrDefault(p.y, 0) + p.val);
            if (i == points.size() - 1 || points.get(i + 1).x > p.x) {
                if (preX > -1) {
                    rt += ((long)preY * (p.x - preX)) % (1000000007);    
                    rt %= (1000000007);
                }
                preY = getY(map);
                preX = p.x;
            }
            
        }
        
        return rt;
    }
    
    private int getY(Map<Integer, Integer> map) {
        int rt = 0, preY = -1, count = 0;
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            if (preY != -1 && count > 0) {
                rt += entry.getKey() - preY;
            }
            count += entry.getValue();
            preY = entry.getKey();
        }
        return rt;
    }
}

Solution #3, Segment Tree O(n * lg n)
Ref: https://leetcode.com/problems/rectangle-area-ii/solution/