505. The Maze II

505. The Maze II

There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the ball's start position, the destination and the maze, find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return -1.

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.

Example 1

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: 12
Explanation: One shortest way is : left -> down -> left -> down -> right -> down -> right.
             The total distance is 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12.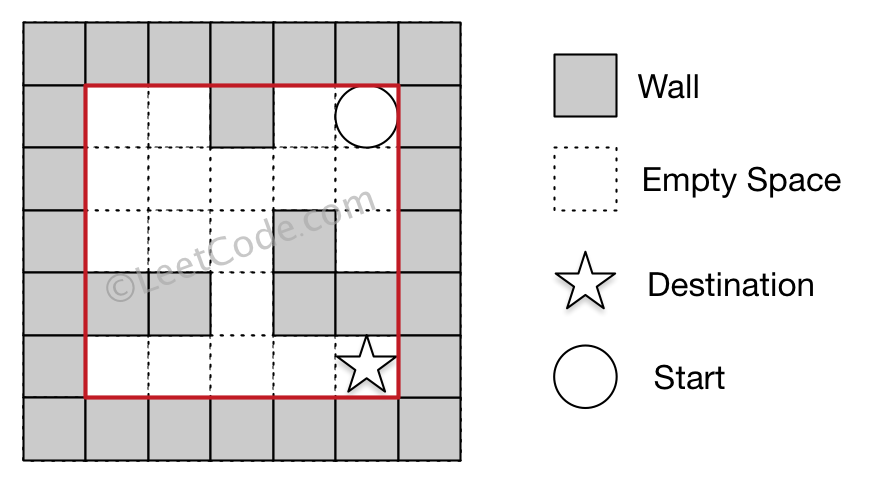

Example 2

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)

Output: -1
Explanation: There is no way for the ball to stop at the destination.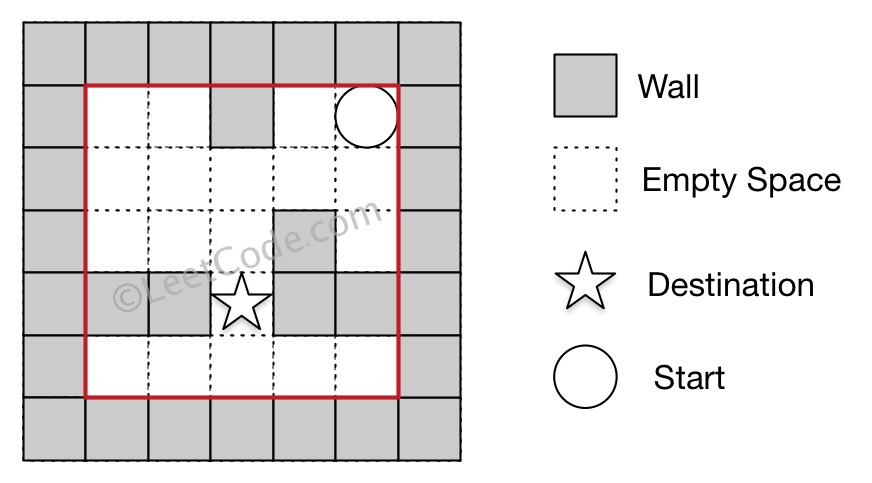

Note:

1. There is only one ball and one destination in the maze.
2. Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
3. The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
4. The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.

------------------
这题其实是一个weighted grahp，vertex是每一个靠墙的点，edge weight是每个vertex之间的距离。所以搜索的方法有dfs，bfs跟dijkstra。复杂度为 (|E| + |V|) * K，K为在每个vertex上的花费

Solution #1, 在Maze I的基础上进行的修改。
1. 因为每一步走的距离都是不等的，所以得保持另一个2d array来记录当前坐标的距离
2. 可以不用预先把记录距离的2d array填满，但是那种算法oj内存溢出，很奇怪
Worst complexity是O((m * n)^2),

class Solution {
    public int shortestDistance(int[][] maze, int[] start, int[] destination) {
        Queue<int[]> que = new LinkedList<>();
        que.add(start);
        int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};
        int[][] dis = new int[maze.length][maze[0].length];
        for (int[] row: dis)
            Arrays.fill(row, Integer.MAX_VALUE);
        dis[start[0]][start[1]] = 0;
        
        while (!que.isEmpty()) {
            int[] pos = que.poll();
            
            for (int[] dir : dirs) {
                int i = 0;
                while (pos[0] + dir[0] * i >= 0 && pos[0] + dir[0] * i < maze.length
                      && pos[1] + dir[1] * i >= 0 && pos[1] + dir[1] * i < maze[0].length
                      && maze[pos[0] + dir[0] * i][pos[1] + dir[1] * i] == 0) {
                    i++;
                }
                i--;
                
                if (dis[pos[0] + dir[0] * i][pos[1] + dir[1] * i] > dis[pos[0]][pos[1]] + i) {
                    dis[pos[0] + dir[0] * i][pos[1] + dir[1] * i] = dis[pos[0]][pos[1]] + i;
                    int[] next = new int[]{pos[0] + dir[0] * i, pos[1] + dir[1] * i};
                    que.add(next);
                }
            }
        }
        
        return dis[destination[0]][destination[1]] == Integer.MAX_VALUE ? -1 : dis[destination[0]][destination[1]];
    }
}

Solution #2, Dijkastra
O(m * n * log(m * n)), queue的大小为 m * n, 每次搜索为lg

下面的实现方式有点问题。检查destination应该在刚刚从queue里出来的时候

class Solution {
    public int shortestDistance(int[][] maze, int[] start, int[] destination) {
        int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};
        int[][] dis = new int[maze.length][maze[0].length];
        
        PriorityQueue<int[]> que = new PriorityQueue<>((a, b) -> a[2] - b[2]);
        que.add(new int[]{start[0], start[1], 0});
        for (int[] row: dis)
            Arrays.fill(row, Integer.MAX_VALUE);
        dis[start[0]][start[1]] = 0;

        while (!que.isEmpty()) {
            int[] pos = que.poll();
            
            for (int[] dir : dirs) {
                int i = 0;
                    
                while (pos[0] + dir[0] * i >= 0 && pos[0] + dir[0] * i < maze.length
                      && pos[1] + dir[1] * i >= 0 && pos[1] + dir[1] * i < maze[0].length
                      && maze[pos[0] + dir[0] * i][pos[1] + dir[1] * i] == 0) {
                    i++;
                }
                i--;
                
                int row = pos[0] + dir[0] * i;
                int col = pos[1] + dir[1] * i;
                
                if (destination[0] == row && destination[1] == col) return pos[2] + i;
                if (dis[row][col] > dis[pos[0]][pos[1]] + i) {
                    
                    dis[row][col] = dis[pos[0]][pos[1]] + i;
                    int[] next = new int[]{ row, col, pos[2] + i};    
                    que.add(next);
                }
            }
        }
        
        return -1;
    }
}