Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.
Rules for a valid pattern:
- Each pattern must connect at least m keys and at most n keys.
- All the keys must be distinct.
- If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
- The order of keys used matters.
Explanation:
| 1 | 2 | 3 | | 4 | 5 | 6 | | 7 | 8 | 9 |
Invalid move:
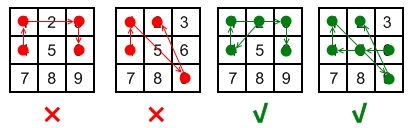
Line 1 - 3 passes through key 2 which had not been selected in the pattern.
4 - 1 - 3 - 6 Line 1 - 3 passes through key 2 which had not been selected in the pattern.
Invalid move:
Line 1 - 9 passes through key 5 which had not been selected in the pattern.
4 - 1 - 9 - 2Line 1 - 9 passes through key 5 which had not been selected in the pattern.
Valid move:
Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern
2 - 4 - 1 - 3 - 6Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern
Valid move:
Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.
6 - 5 - 4 - 1 - 9 - 2Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.
Example:
Input: m = 1, n = 1 Output: 9
注意,andriod机器上,1-8是合法的。所以以下算法把需要额外步数的都记录下来
class Solution {
public int numberOfPatterns(int m, int n) {
int[][] map = new int[10][10];
map[1][3] = map[3][1] = 2;
map[1][7] = map[7][1] = 4;
map[1][9] = map[9][1] = 5;
map[2][8] = map[8][2] = 5;
map[3][7] = map[7][3] = 5;
map[4][6] = map[6][4] = 5;
map[7][9] = map[9][7] = 8;
map[3][9] = map[9][3] = 6;
boolean[] visited = new boolean[10];
visited[0] = true; // 坑
int rt = dfs(map, visited, 1, 1, m, n) * 4; // 1
rt += dfs(map, visited, 2, 1, m, n) * 4; // 2
rt += dfs(map, visited, 5, 1, m, n); // 5
return rt;
}
private int dfs(int[][] map, boolean[] visited, int cur, int len, int m, int n) {
if (len > n) return 0;
int num = 0;
if (len >= m) num++;
visited[cur] = true;
for (int i = 1; i < 10; i++) {
int mid = map[cur][i];
if (!visited[i] && (mid == 0 || visited[mid])) {
num += dfs(map, visited, i, len + 1, m, n);
}
}
visited[cur] = false;
return num;
}
}
如果1-8为非法的写法
class Solution {
private static int[][] dir = {{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,-1},{1,-1},{-1,1}};
public int numberOfPatterns(int m, int n) {
boolean[][] visited = new boolean[3][3];
int num = 0;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
num += helper(visited, 1, i,j,m,n);
}
}
return num;
}
private int helper(boolean[][] visited, int len, int row, int col, int m, int n) {
if (len > n || row < 0 || row >= 3 || col < 0 || col >= 3 || visited[row][col]) return 0;
int num = 0;
if (len >=m && len <= n) num++;
visited[row][col] = true;
for (int i = 0; i < 8; i++) {
int nextR = row + dir[i][0];
int nextC = col + dir[i][1];
num += helper(visited, len + 1, nextR, nextC, m, n);
if (nextR >= 0 && nextR < 3 && nextC >= 0 && nextC < 3 && visited[nextR][nextC]) {
num += helper(visited, len + 1, nextR + dir[i][0], nextC + dir[i][1], m, n);
}
}
visited[row][col] = false;
return num;
}
}
No comments:
Post a Comment