723. Candy Crush

723. Candy Crush

This question is about implementing a basic elimination algorithm for Candy Crush.

Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player's move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:

1. If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
2. After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
3. After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
4. If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.

You need to perform the above rules until the board becomes stable, then return the current board.

Example:

Input:
board = 
[[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]]

Output:
[[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]]

Explanation: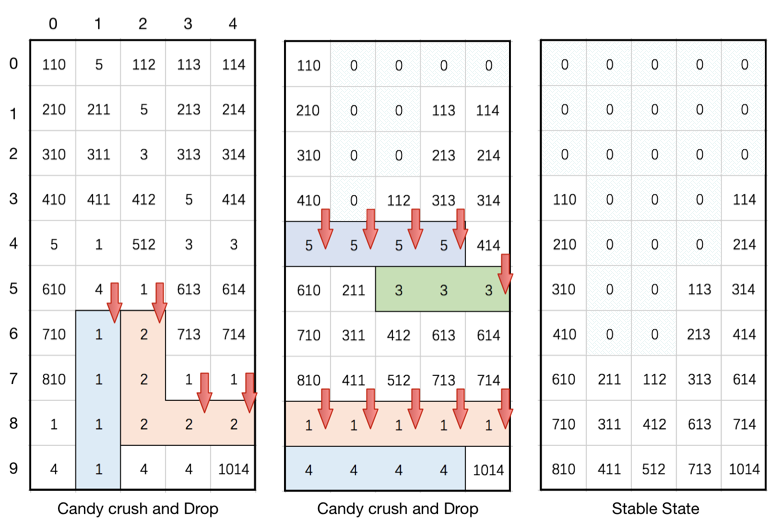 

Note:

1. The length of board will be in the range [3, 50].
2. The length of board[i] will be in the range [3, 50].
3. Each board[i][j] will initially start as an integer in the range [1, 2000].

-----------------
不要想太复杂（again！）
横竖只看3位，然后标记出来
O(m * n * (m + n)), 每次扫描是 m * n, 方向上每个方向最多只能塌陷m次和n次

class Solution {
    public int[][] candyCrush(int[][] board) {
        boolean found = true;
        int m = board.length, n = board[0].length;
        
        while (found) {
            found = false;
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n - 2; j++) {
                    int val = Math.abs(board[i][j]);
                    if (val != 0 && Math.abs(board[i][j + 1]) == val 
                       && Math.abs(board[i][j + 2]) == val) {
                        
                        board[i][j] = board[i][j + 1] = board[i][j + 2] = -val;
                        found = true;
                    }
                }
            }
            
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m - 2; j++) {
                    int val = Math.abs(board[j][i]);
                    if (val != 0 && Math.abs(board[j + 1][i]) == val 
                       && Math.abs(board[j + 2][i]) == val) {
                        
                        board[j][i] = board[j + 1][i] = board[j + 2][i] = -val;
                        found = true;
                    }
                }
            }
            
            for (int c = 0; c < n; ++c) {
                int wr = m - 1;
                for (int r = m-1; r >= 0; --r)
                    if (board[r][c] > 0)
                        board[wr--][c] = board[r][c];
                while (wr >= 0)
                    board[wr--][c] = 0;
            }
        }
        
        return board;
    }
    
    
}