684. 685. Redundant Connection, Redundant Connection II

684. Redundant Connection

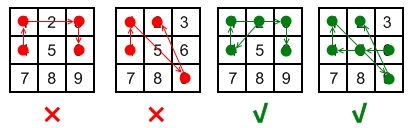
In this problem, a tree is an undirected graph that is connected and has no cycles.

The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, ..., N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.

The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.

Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.

Example 1:

Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given undirected graph will be like this:
  1
 / \
2 - 3

Example 2:

Input: [[1,2], [2,3], [3,4], [1,4], [1,5]]
Output: [1,4]
Explanation: The given undirected graph will be like this:
5 - 1 - 2
    |   |
    4 - 3

Note:

The size of the input 2D-array will be between 3 and 1000.

Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.

Update (2017-09-26):
We have overhauled the problem description + test cases and specified clearly the graph is an undirected graph. For the directedgraph follow up please see Redundant Connection II). We apologize for any inconvenience caused.

-----------------------
Union Find. DFS 也可以做，只是题意要求返回在原数组里最靠后的一位，所以UF更简单

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        int[] ids = new int[n + 1];
        int[] sizes = new int[n + 1];
        
        for (int i = 1; i <= n; i++) {
            ids[i] = i;
            sizes[i] = 1;
        }
        
        for (int[] e : edges) {
            int r1 = find(ids, e[0]);
            int r2 = find(ids, e[1]);
            if (r1 == r2) return e;
            
            union(r1,r2,ids,sizes);
        }
        
        return null;
    }
    
    private void union(int id1, int id2, int[] ids, int[] sizes) {
        if (sizes[id1] > sizes[id2]) {
            sizes[id1] += sizes[id2];
            ids[id2] = id1;
        }else {
            sizes[id2] += sizes[id1];
            ids[id1] = id2;
        }
    }
    
    private int find(int[] ids, int id) {
        while (ids[id] != id) {
            ids[id] = ids[ids[id]];
            id = ids[id];
        }
        
        return id;
    }
}

685. Redundant Connection II

In this problem, a rooted tree is a directed graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents.

The given input is a directed graph that started as a rooted tree with N nodes (with distinct values 1, 2, ..., N), with one additional directed edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.

The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] that represents a directed edge connecting nodes u and v, where u is a parent of child v.

Return an edge that can be removed so that the resulting graph is a rooted tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array.

Example 1:

Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given directed graph will be like this:
  1
 / \
v   v
2-->3

Example 2:

Input: [[1,2], [2,3], [3,4], [4,1], [1,5]]
Output: [4,1]
Explanation: The given directed graph will be like this:
5 <- 1 -> 2
     ^    |
     |    v
     4 <- 3

Note:

The size of the input 2D-array will be between 3 and 1000.

Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.

-----------------------

因为是tree ＋ 1个extra edge，所以分2种情况：

1. 所有的结点都有parent(包括root)。这有个环。

或

2. 有一个结点有2个parent指向。这里还可以分2种情况。

思路是先确定是哪种情况，2的话找出那2个parent的指向，然后断开第2个。进行正常的UF操作，如果碰到是2的情况，那说明先前存的第1个parent指向是extra edge。如果碰到的都是是1的情况，则当前的edge是多余。

如果没有相同的父节点，说明之前断开第2个edge是多余的（环被打断）

同样的，这题可以用DFS做，也得先preprocess

class Solution {
    public int[] findRedundantDirectedConnection(int[][] edges) {
        int n = edges.length;
        int[] ids = new int[n + 1];
        int[][] cands = new int[2][2];
        
        for (int[] e : edges) {            
            if (ids[e[1]] != 0) {
                cands[0] = new int[]{ids[e[1]], e[1]};
                cands[1] = new int[]{e[0], e[1]};
                e[0] = 0;
            }else {
                ids[e[1]] = e[0];    
            }
        }
        
        for (int i = 1; i <= n; i++) 
            ids[i] = i;
        
        for (int[] e : edges) {
            if (e[0] == 0) continue;
            int r1 = find(ids, e[0]);
            int r2 = e[1];
            if (r1 == r2) {
                if (cands[0][0] == 0) return e;
                return cands[0];
            }
            
            ids[r2] = r1;
        }
        
        return cands[1];
    }
    
    private int find(int[] ids, int id) {
        while (ids[id] != id) {
            ids[id] = ids[ids[id]];
            id = ids[id];
        }
        
        return id;
    }
}

750. Number Of Corner Rectangles

750. Number Of Corner Rectangles

Given a grid where each entry is only 0 or 1, find the number of corner rectangles.

A corner rectangle is 4 distinct 1s on the grid that form an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1s used must be distinct.

Example 1:

Input: grid = 
[[1, 0, 0, 1, 0],
 [0, 0, 1, 0, 1],
 [0, 0, 0, 1, 0],
 [1, 0, 1, 0, 1]]
Output: 1
Explanation: There is only one corner rectangle, with corners grid[1][2], grid[1][4], grid[3][2], grid[3][4].

Example 2:

Input: grid = 
[[1, 1, 1],
 [1, 1, 1],
 [1, 1, 1]]
Output: 9
Explanation: There are four 2x2 rectangles, four 2x3 and 3x2 rectangles, and one 3x3 rectangle.

Example 3:

Input: grid = 
[[1, 1, 1, 1]]
Output: 0
Explanation: Rectangles must have four distinct corners.

Note:

1. The number of rows and columns of grid will each be in the range [1, 200].
2. Each grid[i][j] will be either 0 or 1.
3. The number of 1s in the grid will be at most 6000.

----------------------------
找出每两个row之间的矩形个数。
O(m^2 * n)
可以优化的地方是把计算第一个row的时候把1额外开一个数组存好

class Solution {
    public int countCornerRectangles(int[][] grid) {
        
        int rt = 0;
        for (int i = 0; i < grid.length - 1; i++) {
            for (int j = i + 1; j < grid.length; j++) {
                int count = 0;
                for (int col = 0; col < grid[0].length; col++) {
                    if (grid[i][col] == 1 && grid[j][col] == 1) count++;
                }
                
                if (count > 0) rt += count * (count - 1) / 2;
            }
        }
        
        return rt;
    }
}

另一种算法 ref: https://leetcode.com/problems/number-of-corner-rectangles/solution/

939. Minimum Area Rectangle

939. Minimum Area Rectangle

Given a set of points in the xy-plane, determine the minimum area of a rectangle formed from these points, with sides parallel to the x and y axes.

If there isn't any rectangle, return 0.

Example 1:

Input: [[1,1],[1,3],[3,1],[3,3],[2,2]]
Output: 4

Example 2:

Input: [[1,1],[1,3],[3,1],[3,3],[4,1],[4,3]]
Output: 2

Note:

1. 1 <= points.length <= 500
2. 0 <= points[i][0] <= 40000
3. 0 <= points[i][1] <= 40000
4. All points are distinct.

------------------------
找对角的点
O(n^2)

class Solution {
    public int minAreaRect(int[][] points) {
        Map<Integer, Set<Integer>> map = new HashMap<>();
        
        for (int[] p : points) {
            if (!map.containsKey(p[0])) {
                map.put(p[0], new HashSet<>());
            }
            map.get(p[0]).add(p[1]);
        }
        
        int min = Integer.MAX_VALUE;
        for (int[] p1 : points) {
            for (int[] p2 : points) {
                if (p1[0] == p2[0] || p1[1] == p2[1]) continue;
                
                if (map.get(p1[0]).contains(p2[1]) && map.get(p2[0]).contains(p1[1])) {
                    min = Math.min(Math.abs(p1[0] - p2[0]) * Math.abs(p1[1] - p2[1]), min);
                }
            }
        }
        
        return min == Integer.MAX_VALUE ? 0 : min;
    }
}

351. Android Unlock Patterns

351. Android Unlock Patterns

Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.

Rules for a valid pattern:

1. Each pattern must connect at least m keys and at most n keys.
2. All the keys must be distinct.
3. If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
4. The order of keys used matters.

Explanation:

| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |

Invalid move: 4 - 1 - 3 - 6 
Line 1 - 3 passes through key 2 which had not been selected in the pattern.

Invalid move: 4 - 1 - 9 - 2
Line 1 - 9 passes through key 5 which had not been selected in the pattern.

Valid move: 2 - 4 - 1 - 3 - 6
Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern

Valid move: 6 - 5 - 4 - 1 - 9 - 2
Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.

Example:

Input: m = 1, n = 1
Output: 9

---

------------------------
注意，andriod机器上,1-8是合法的。所以以下算法把需要额外步数的都记录下来

class Solution {
    public int numberOfPatterns(int m, int n) {
        int[][] map = new int[10][10];
        map[1][3] = map[3][1] = 2;
        map[1][7] = map[7][1] = 4;
        map[1][9] = map[9][1] = 5;
        map[2][8] = map[8][2] = 5;
        map[3][7] = map[7][3] = 5;
        map[4][6] = map[6][4] = 5;
        map[7][9] = map[9][7] = 8;
        map[3][9] = map[9][3] = 6;
        boolean[] visited = new boolean[10];
        visited[0] = true; // 坑
        
        int rt = dfs(map, visited, 1, 1, m, n) * 4; // 1
        rt += dfs(map, visited, 2, 1, m, n) * 4; // 2
        rt += dfs(map, visited, 5, 1, m, n); // 5
        
        return rt;
    }
    
    private int dfs(int[][] map, boolean[] visited, int cur, int len, int m, int n) {
        if (len > n) return 0;
        int num = 0;
        if (len >= m) num++;
        
        visited[cur] = true;
        for (int i = 1; i < 10; i++) {
            int mid = map[cur][i];
            
            if (!visited[i] && (mid == 0 || visited[mid])) {
                num += dfs(map, visited, i, len + 1, m, n); 
            }
        }
        visited[cur] = false;
        
        return num;
    }
}

如果1-8为非法的写法

class Solution {
    
    private static int[][] dir = {{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,-1},{1,-1},{-1,1}};

    public int numberOfPatterns(int m, int n) {
        boolean[][] visited = new boolean[3][3];
        int num = 0;
        
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                num += helper(visited, 1, i,j,m,n);        
            }
        }
        
        return num;
    }
    
    private int helper(boolean[][] visited, int len, int row, int col, int m, int n) {

        if (len > n || row < 0 || row >= 3 || col < 0 || col >= 3 || visited[row][col]) return 0;
        int num = 0;
        if (len >=m && len <= n) num++;
        
        visited[row][col] = true;
            
        for (int i = 0; i < 8; i++) {
            int nextR = row + dir[i][0];
            int nextC = col + dir[i][1];
            num += helper(visited, len + 1, nextR, nextC, m, n);
            if (nextR >= 0 && nextR < 3 && nextC >= 0 && nextC < 3 && visited[nextR][nextC]) {
                num += helper(visited, len + 1, nextR + dir[i][0], nextC + dir[i][1], m, n);
            }
        }
        
        visited[row][col] = false;
        return num;
    }
}

809. Expressive Words

809. Expressive Words

Sometimes people repeat letters to represent extra feeling, such as "hello" -> "heeellooo", "hi" -> "hiiii".  Here, we have groups, of adjacent letters that are all the same character, and adjacent characters to the group are different.  A group is extended if that group is length 3 or more, so "e" and "o" would be extended in the first example, and "i" would be extended in the second example.  As another example, the groups of "abbcccaaaa" would be "a", "bb", "ccc", and "aaaa"; and "ccc" and "aaaa" are the extended groups of that string.

For some given string S, a query word is stretchy if it can be made to be equal to S by extending some groups.  Formally, we are allowed to repeatedly choose a group (as defined above) of characters c, and add some number of the same character c to it so that the length of the group is 3 or more.  Note that we cannot extend a group of size one like "h" to a group of size two like "hh" - all extensions must leave the group extended - ie., at least 3 characters long.

Given a list of query words, return the number of words that are stretchy. 

Example:
Input: 
S = "heeellooo"
words = ["hello", "hi", "helo"]
Output: 1
Explanation: 
We can extend "e" and "o" in the word "hello" to get "heeellooo".
We can't extend "helo" to get "heeellooo" because the group "ll" is not extended.

Notes:

• 0 <= len(S) <= 100.
• 0 <= len(words) <= 100.
• 0 <= len(words[i]) <= 100.
• S and all words in words consist only of lowercase letters

-----------------
又又又一道说不清题意题

解法：
对字母每次出现的连续次数（个数）做对比
一些例子:
fffe, ffe -> true
fffe,fffe -> true
ffe, fe -> false
ffe, ffe -> true
O(m * n)

class Solution {
    public int expressiveWords(String S, String[] words) {
        int count = 0;
        for (String w : words) {
            if (helper(S, w)) count++;
        }
        
        return count;
    }
    
    private boolean helper(String s, String w) {
        int i = 0, j = 0;
        int m = s.length(), n = w.length();
        
        while (i < m && j < n) {
            char c1 = s.charAt(i);
            char c2 = w.charAt(j);
            
            if (c1 != c2) return false;
            int count1 = getCount(s, i);
            int count2 = getCount(w, j);
            
            if ((count1 == 2 && count2 == 1) 
                || (count1 < count2)) return false;
            i += count1;
            j += count2;
        }
        
        
        return i == m && j == n;
    }
    
    private int getCount(String s, int i) {
        int count = 1;
        i++;
        while (i < s.length()) {
            if (s.charAt(i) == s.charAt(i - 1)) count++;
            else break;
            i++;
        }
        
        return count;
    }
}

727. Minimum Window Subsequence

727. Minimum Window Subsequence

Given strings S and T, find the minimum (contiguous) substring W of S, so that T is a subsequence of W.

If there is no such window in S that covers all characters in T, return the empty string "". If there are multiple such minimum-length windows, return the one with the left-most starting index.

Example 1:

Input: 
S = "abcdebdde", T = "bde"
Output: "bcde"
Explanation: 
"bcde" is the answer because it occurs before "bdde" which has the same length.
"deb" is not a smaller window because the elements of T in the window must occur in order.

Note:

• All the strings in the input will only contain lowercase letters.
• The length of S will be in the range [1, 20000].
• The length of T will be in the range [1, 100].

------------------------
Solution #1, 指针
找到一个匹配之后，以结尾为起始点，倒退着往前找。这样找到的是在[i, j]里最短的符合要求的substring。最坏结果是找到跟原来一摸一样的。
O(m * n) time. 对Complexity的需要研究一下

ref： https://leetcode.com/problems/minimum-window-subsequence/discuss/109356/JAVA-two-pointer-solution-(12ms-beat-100)-with-explaination

class Solution {
    public String minWindow(String s, String t) {
        int si = 0, ti = 0;
        String rt = s + "123";
        while (si < s.length()) {
            if (s.charAt(si) == t.charAt(ti)) {
                if (ti == t.length() - 1) {
                    int end = si;                    
                    while (ti >= 0) {
                        while (s.charAt(si) != t.charAt(ti)) {
                            si--;
                        }
                        ti--;
                        si--;
                    }
                    
                    si++;
                    if (rt.length() > end - si + 1) {
                        rt = s.substring(si, end + 1);
                    }
                }
                ti++;
            }
            
            si++;
        }
        
        return rt.equals(s + "123") ? "" : rt;
    }
}

Solution #2, DP
dp[i][j] = k, i为T的index，j为S的index，k为以[0,i]，[0,j]这2段substring最小的起点在s上
如果s[j] == t[i], dp[i][j]那可以借用dp[i - 1][j - 1]时的起点
如果s[j] ！= t[i]，可以借用dp[i][j - 1]

注意dp的初始赋值

class Solution {
    public String minWindow(String s, String t) {
        int n = s.length(), m = t.length();
        int[][] dp = new int[m][n];
        for (int i = 0; i < n; i++) {
            if (s.charAt(i) == t.charAt(0)) dp[0][i] = i;
            else if (i > 0) dp[0][i] = dp[0][i - 1];
            else dp[0][i] = -1;
        }

        for (int i = 1; i < m; i++) {
            dp[i][0] = -1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1 ; j < n; j++) {
                if (i > j) dp[i][j] = -1;
                else {
                    if (t.charAt(i) == s.charAt(j)) {
                        dp[i][j] = dp[i - 1][j - 1];
                    }else {
                        dp[i][j] = dp[i][j - 1];
                    }
                }
            }
        }

        int min = n;
        String rt = "";
        for (int i = 0; i < n; i++) {
            if (dp[m - 1][i] == -1) continue;
            if (min > i - dp[m - 1][i] + 1) {
                rt = s.substring(dp[m - 1][i], i + 1);
                min = i - dp[m - 1][i] + 1;
            }
        }

        return rt;
    }
}